In my year two days, I think I was seven then, my brother and I always seemed to be the last to be collected from school. Our usual spot was the bench near the entrance, eyes fixed on the gate, waiting for the familiar sight of either mom or dad coming to fetch us. Even though we could have easily walked home, our parents wanted us to stay on school grounds until they could come and pick us up. It was a safety thing, we knew.

Our parents had their hands full with two jobs each, so you can imagine the balancing act they had to perform just to make sure we were picked up on time. Our bench had a view of a busy road, and to keep ourselves entertained, we invented games. One of the games was guessing when the next yellow car would zoom by. The one who guessed closest to the actual time was declared the winner.

It's funny how life's little moments can connect to bigger ideas. In this case, the Exponential distribution seems to link nicely to our childhood game. And so, I want to focus on Exponential distribution in this blog. It has an interesting connection to Poisson distribution. I'll explain what that is a bit later.

In this blog, we'll explore the following:

• What is Exponential Distribution?
• Relationship between Poisson and Exponential Distribution
• Worked Example of Exponential Distribution
• Characteristics of Exponential Distribution
• Application of Exponential Distribution

What is Exponential Distribution?

The exponential distribution is a type of probability distribution used in statistics. It's often used to model the time between events that happen randomly at a constant average rate.

Let's take the game I played with my brother as an example. Say, I know that, on average, a yellow car would pass us by every 15 minutes. The exponential distribution can help predict how long we might have to wait for the next yellow car.

To explain it in another way, the exponential distribution helps us understand the likelihood of waiting a certain amount of time before the next yellow car appears.

Relationship Between Poisson & Exponential Distribution

Exponential distribution and the Poisson distribution have an interesting relationship. They are closely related and complementary in some contexts.
Exponential distribution models the time between events in a Poisson process, while Poisson distribution counts events within a fixed interval. If you're wondering what the Poisson process is, it is a counting process where we count the occurrence of certain events that appear to happen at a certain rate but completely at random, without a particular structure.

Let's look at this with the example of guessing when the next yellow car will zoom by:

In the case of Poisson distribution, we would try to predict the likelihood of guessing, say, eight yellow cars passing by in one hour, given that we see about ten yellow cars every hour.

Now, with exponential distribution, we switch this around. On average, ten yellow cars pass by every hour; the exponential distributions will help us figure out questions like how long we might have to wait for the next yellow car to zoom by. It tells you the chances of waiting, say, less than 15 minutes or more than 30 minutes for that next event to occur.

Worked Example of Exponential Distribution

Let's look at the two formulas used in exponential distribution: Probability Density Function (PDF) and Cumulative Distribution Function (CDF). At the risk of sounding like a broken record, I'm still going to rehash the importance of understanding these two terms in Probability Distribution and Statistics.

Not just these two terms, but if you want to build a strong foundation in understanding various probability distributions, you must grasp and remember the following key concepts:

• Discrete vs. Continuous Probability Distribution: Familiarize yourself with the distinction between discrete and continuous probability distributions. Understand the fundamental differences between them.
• PMF, PDF, and CDF: Acquaint yourself with the concepts of Probability Mass Function (PMF), Probability Density Function (PDF), and Cumulative Distribution Function (CDF). Recognize their roles and differences in probability distribution analysis.
• Total Probability: Recognize that the sum of probabilities in any probability distribution always equals 1 (or 100%).

If you feel your understanding of these concepts is not quite solid, I recommend revisiting this blog: Probability Distributions for Beginners. It provides a beginner-friendly explanation that can help clarify any uncertainties and strengthen your understanding of these essential concepts.

Sorry, I digress; back to the PDF and CDF of exponential Distribution.
This is what the formula and respective graphs look like.

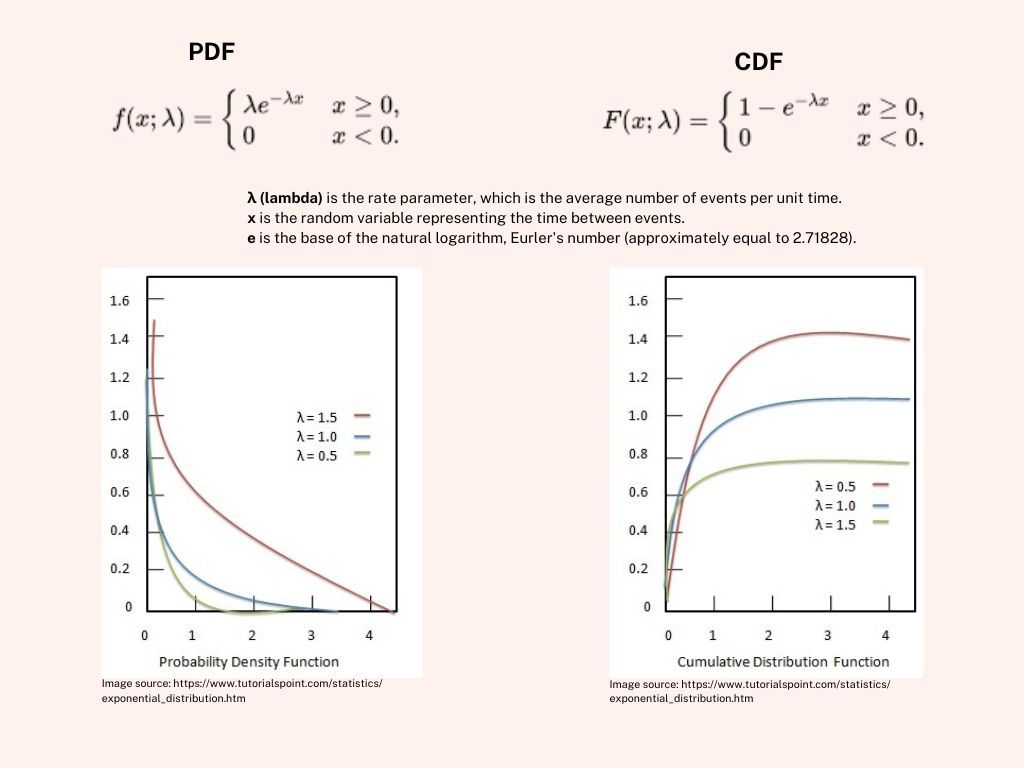
You may note that for each PDF and CDF, where that x random variable is < 0, the probability is 0. Hold on to the observation. I'll come back to it and explain why. It's a unique property of exponential distribution.

Now, this hasn't been said anywhere, at least I've not come across it, but I've noticed thatit's often more common to work with the CDF rather than the PDF when it comes to exponential distribution. I'm not sure why that's the case. If you know or find out the reason why that's the case, do share.

With that said, our example will require us to use CDF.

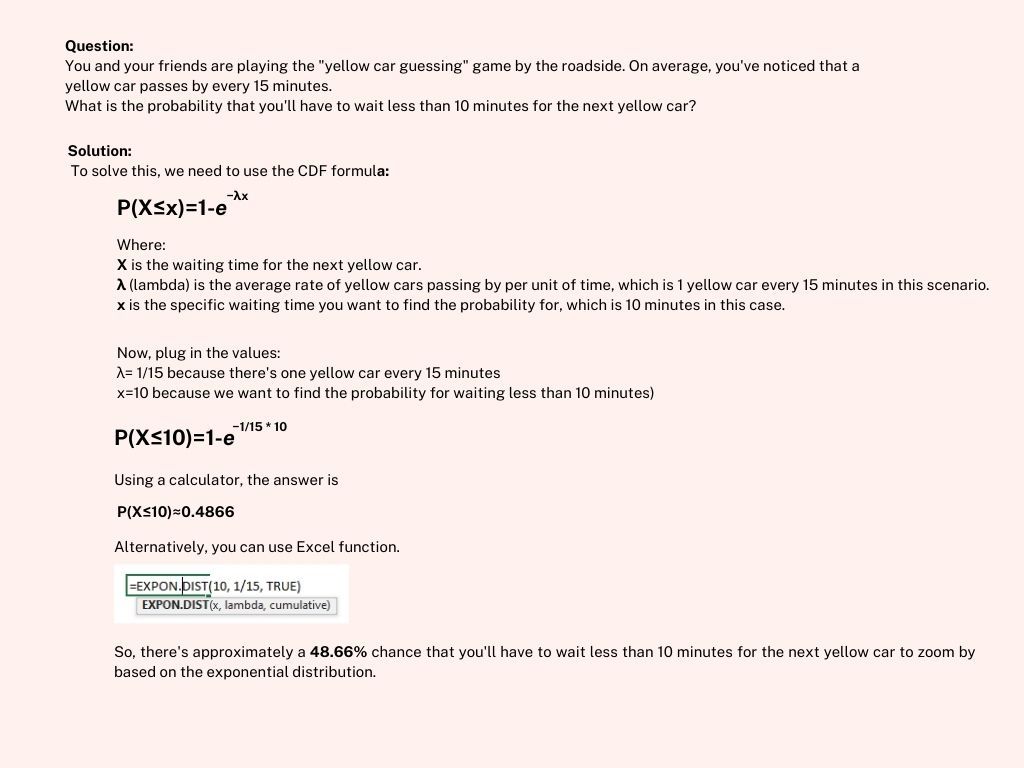
Characteristics of Exponential Distribution

Exponential distribution has two interesting characteristics:

Memoryless-ness Property: The exponential distribution exhibits the memoryless-ness property, a unique characteristic. This property states that the conditional probability of an event occurring after a certain time, given that it has not occurred up to that time, is the same as the probability of the event occurring in the original time interval. So, this is saying the past doesn't affect the future.

For example, let's say you're waiting for a bus, and it's running late. The memoryless-ness property means that the probability of the bus arriving in the next 10 minutes, given that you've already waited for 20 minutes, is the same as if you had just arrived at the bus stop and started waiting. It doesn't matter how long you've already waited; the bus's arrival time is still the same as when you first arrived.

This memoryless-ness makes it easier to model and analyze random processes. It allows us to treat each time interval independently, as if starting from scratch each time. However, its benefit is also its limitation. We know this is not an accurate representation of all real-world situations. In some cases, the past history of events can influence future events' likelihood. So, while memoryless-ness simplifies calculations, it may not be suitable for every scenario involving time and events.

Non-negative values: Another property it has is non-negative values. Recall that I mentioned holding on to the observation that the probability is zero when the random value x is 0. The x represents the time between events or the duration of some processes. Since time and duration cannot be a negative value, and so x cannot be negative. For example, the time between the arrivals of customers at a store, the time between phone calls at a customer service centre, or the time it takes for a component to fail in a manufacturing process—all of these are inherently non-negative.

Application of Exponential Distribution

The exponential distribution has several real-world applications. Here are a few:

Physics - Radioactive Decay: In nuclear physics, the exponential distribution is employed to model the time it takes for radioactive substances to decay. It helps scientists predict when a given radioactive atom will disintegrate.

Engineering - Quality Control: On an assembly line where products are being manufactured, the exponential distribution can be used to estimate the time between receiving defective parts. This is valuable for quality control and production efficiency.

Finance - Default Probability: In finance, the exponential distribution is a tool for assessing the likelihood of a company defaulting on its financial obligations. It can also be applied to evaluate the probability of a certain number of defaults occurring within a specific timeframe, aiding in risk assessment for portfolios of financial assets.

Ok, that's a wrap. I hope you learned a thing or two about exponential distribution. Who would have guessed that waiting for yellow cars could lead us on such an exploration? Life offers delightful surprises and intriguing links between the ordinary and the extraordinary.