Linear Algebra for AI Beginners
A week ago, I began my AI learning journey.
While building AI has become easier with tools like no-code platforms and “vibe coding,” I don’t want to just use them, I want to understand them.
I believe that an aspect of creativity comes from knowing how things work beneath the surface. When you understand the fundamentals well, you can troubleshoot, reason more clearly, and come up with original solutions.
So here I am, back to math. Specifically, Linear Algebra, the foundation of how machines represent and transform data.
This post is my way of revisiting those core ideas and making sense of the math that makes machines think.

What you’re seeing here is how a computer “sees” an image, not as a photo, but as a matrix of numbers.
Each pixel in the picture is represented by a value between 0 (black) and 1 (white), showing how bright that spot is. When we convert a color image to grayscale, the red, green, and blue values for each pixel are blended into one brightness value.
The result is a grid of numbers that looks like the cat image you see here. This is how AI and computer vision systems process images as numerical data that can be transformed, analyzed, and learned from using Linear Algebra. Once you see it this way, it’s easy to understand why learning Linear Algebra matters so much.
To build that understanding, let’s look at what we’ll cover in this post.
What We'll Cover
This post focuses on Linear Algebra, one of the three mathematical pillars of AI (alongside Calculus and Statistics).
We’ll explore:
-
What Linear Algebra is and why it’s the language of AI
-
Its building blocks: scalars, vectors, matrices, dot products, and transformations and how they are applied in AI.
-
How Linear Algebra connects with Calculus and Statistics
What is Linear Algebra?
Linear Algebra studies vectors, matrices, and transformations, how collections of numbers interact, combine, and change.
Every type of data, whether it be text, images, audio, is ultimately represented as numbers. Linear Algebra provides the framework for expressing, comparing, and transforming those numbers so computers can understand them.
Think of it as the language of data and data movement.
When you rotate, scale, or flip an image, you’re transforming all its pixel values in a coordinated way. The same principle lets AI “look at data from different angles” much like how we turn an object in our hands to examine it.
The Building Blocks of Linear Algebra
Linear Algebra can sound intimidating, but it’s simply the math of how machines represent and transform information.
Let’s unpack its key components.
1. Scalars
A scalar is a single number like 3, 0.01, or –7.
The term comes from scale, because scalars stretch or shrink other quantities.
If you multiply a vector [3, 4] by 2, you get [6, 8].
The direction stays the same, but the length doubles, it’s been scaled.
Why it matters in AI?
Scalars quietly control nearly everything that happens inside a model:
- Learning rate: how big a step the model takes when updating itself.
- Loss value: how far off the model’s predictions are a single number the model tries to minimize.
- Weights: numbers that determine how strongly each input influences the output.
Small, simple numbers but they steer an entire network’s behaviour.
2. Vectors
A vector is something with magnitude and direction. If you studied physics, this is the definition you might be familiar with. In computer science this also applies and is represented as a list of numbers. But Danni where does the direction come in?
Lets look at an example. This is a simple 2 dimensional vector [3, 4]. It means 3 steps right and 4 steps up on your xy plane (Cartesian plane).
In AI, we use vectors, a list of numbers,to represent information such as texts, images, customer, product in a meaningful way.
For example, "cat" and "dog" can each be represented by 300 dimensional vectors that capture their meaning.
The closer these vecto9rs point in the same direction, the more similar they are semantically.
In short: vectors represent information.
3. Matrices
A matrix is a grid of numbers, like your spreadsheet.
Each row or column can present a vector.
Matrices are where most of the “action” happens in AI.
When you multiply a matrix by a vector (or another matrix), you’re transforming that data — combining, rotating, or scaling it in structured ways.
In image processing, a small 3×3 matrix can blur or sharpen an image by applying weighted transformations to pixel neighborhoods.
We apply these transformation to reveal structure and meaning inside the information. You can think of it like asking different questions to understand different sides of a person.
4. Dot Products
The dot product takes two vectors and gives you one number that tells how much they’re pointing in the same direction.
- Point the same way → big positive number
- Point opposite ways → negative number
- Not related → close to zero
It’s like asking, “How much do these two things agree?”
In AI, that’s how math turns into meaning.
For example, Netflix represents both users and movies as vectors.
If the dot product between them is high, it means their patterns line up and the system reads that as “you’ll probably like this movie.”
5. Matrix Multiplication & Linear Transformations
This is where Linear Algebra truly comes alive.
Whenever data moves through an AI system, it’s being reshaped through matrix multiplication, a process that performs linear transformations.
What Matrix Multiplication Means?
A matrix defines how to mix and combine inputs.
When multiplied by a vector or another matrix, it creates a new output, a transformed version of your data.
Think of it like a recipe:
You take ingredients (inputs), mix them in specific proportions (matrix weights), and get a new dish (output).
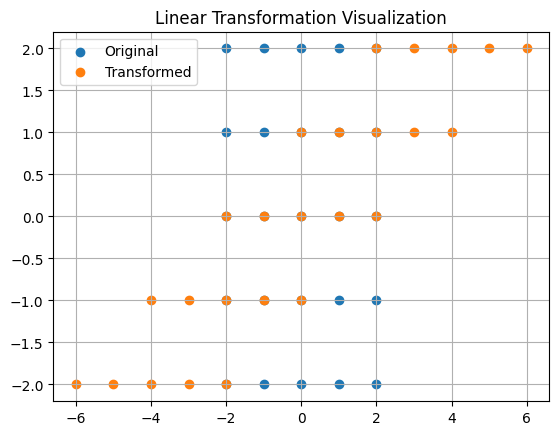
What a Linear Transformation Does?
A linear transformation is simply the effect of that multiplication.
It stretches, rotates, or scales your data in predictable ways, no bending or warping.
If you plotted your data points on a graph, they’d still line up neatly, just in a different position or orientation.
This predictability makes linear transformations powerful tools for discovering structure and patterns in data.
Why It Matters for AI?
Before any “intelligence” happens, data must first be represented and reshaped into forms a machine can work with.
That’s what matrix multiplication does, it turns raw numbers (pixels, words, measurements) into structured signals that later stages of AI can interpret and learn from.
Every modern AI system starts here, with data being linearly transformed.
How Linear Algebra Connects to Calculus and Statistics
Linear Algebra doesn’t work in isolation.
Together with Calculus and Statistics, it forms the Math Triangle of AI.
| Math Branch | What It Adds | In AI |
|---|---|---|
| Linear Algebra | Structure & representation | How data is stored and transformed. Vectors and matrices represent everything, from images to words, and reveal patterns. |
| Calculus | Change & optimization | How models learn, adjusting weights step by step through gradients to minimize loss. |
| Statistics & Probability | Uncertainty & inference | How models reason about noisy or incomplete data, recognize patterns, and make predictions. |
Together, they form an elegant three-part engine:
Combined, they let machines see (represent), learn (optimize), and decide (predict).
Key Takeaways
- Linear Algebra makes data visible. It’s how AI stores and transforms information.
- Calculus makes learning possible. It lets AI adjust and improve.
- Statistics makes decisions intelligent. It helps AI reason under uncertainty.
Together, they form the mathematical backbone of intelligence.
Once you see vectors, matrices, and transformations as ways of expressing meaning, the math stops feeling abstract, it becomes the foundation of how machines think.
If you grasp scalars, vectors, matrices, dot products, and transformations, you already understand good portion of the math that powers today’s AI.
Next up: Calculus for AI Beginners, how machines learn through change. Stay tuned! 🤓

