A couple of weeks back, while brushing up on my Monte Carlo Simulation knowledge for the blog post, I stumbled upon the term "Markov Chain" in some YouTube recommendations. Naturally, it piqued my curiosity, so I decided to have a look. Surprisingly, it turned out to be quite cool. It's another powerful statistical concept with tons of real-world applications, especially for modelling random processes.

I was a bit freaked out by the formal definition of the Markov chain and the mathematical equations- it's quite intimidating, but with the help of an example, the concept is surprisingly easy to understand. So, in this blog, I will share what I've learned. Don't worry, I'll keep math to a minimum.

So, in this blog, we will look at:

• What is the Markov Chain?
• An Example of Markov Chain
• Key Principles of Markov Chain
• Applications of Markov Chain

What is the Markov Chain?

Markov chain is named after the Russian mathematician Andrey Markov, who introduced this concept in the early 20th Century. At its core, a Markov Chain is a mathematical model that describes a sequence of events where the probability of each event depends solely on the state achieved in the previous event. Imagine the game Monopoly; your next move is determined by where you currently are on the board, not by the series of moves that got you there. In the realm of mathematics and statistics, Markov chains have proven invaluable, especially in predicting the behaviour of systems over time. They've found applications in diverse areas such as economics, physics, and computer science. We will look at a few of its applications in the Applications of Markov Chains section.

An Example of Markov Chain

Let's look at an example of Markov Chains that delves into emotional states. This inspiration stemmed from my own mood swings this week, courtesy of a delightful hormonal rollercoaster. 😅

Imagine we're examining the emotional states of a person named Danni. Danni can experience four distinct emotional states: joy, sadness, fear, and anger. Whenever you observe Danni, you can easily tell which of these four emotional states she's in, and it's always one of these options.

Now, let's say you're curious about predicting what Danni's next emotional state will be based on her current one. You suspect there might be some patterns or transition probabilities governing these emotional shifts. So, being the diligent observer you are, you start collecting data by closely monitoring Danni's emotional states over an extended period.

From your meticulous observations, you compile the following transition probabilities, neatly organized in the "Transition Matrix" below:

Here is how to interpret the Transition Matrix:

If Danni is currently in a state of "Joy" today, there's a 60% chance she'll still be joyful tomorrow, a 20% chance she'll transition to sadness, a 10% chance for fear, and a 10% chance for anger.

If she is sad, there's a 30% chance she'll be joyful tomorrow, a 40% chance she'll remain sad, a 20% chance for fear, and a 10% chance for anger. And so on for each emotional state.

It's important to note that the probabilities in each row of the matrix add up to 1 (or 100%), ensuring that one of these outcomes must happen.

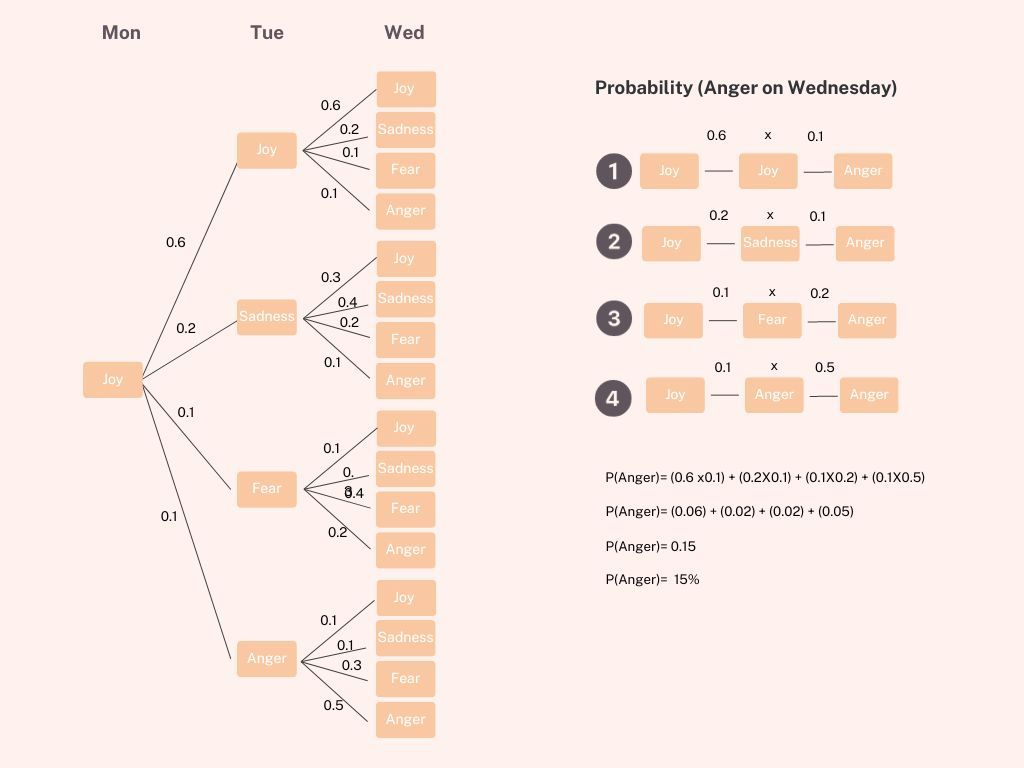
Now, let's get to the fun part of using this Markov Chain to predict the probability of Danni being angry on Wednesday, assuming she started the week with joy on Monday. Why Wednesday, you ask? Well, you both happen to be in the office, and you'd like to gauge whether it's wise to approach her or give her some space. 😆

Using the transition probabilities, we'll start with Danni being joyful on Monday, and then we'll calculate the probability of her being in each emotional state on subsequent days until Wednesday. By applying these probabilities iteratively, we can estimate the likelihood of Danni being angry when you see her in the office. So, let's crunch those numbers and see what the Markov Chain reveals!

In the diagram below, I've transformed the transition matrix into a tree diagram to help us figure out the probability of Danni being angry on Wednesday. There are four distinct pathways that lead to this outcome. We'll compute the probability for each of these paths and then sum them up to arrive at the overall probability, which, as it turns out, is a mere 15%. So, the odds are in your favour – no need to dodge Danni at the office! 😅

Key Principles of Markov Chains

Now, let's delve into some essential principles of Markov Chains. Here are three key ones to keep in mind:

Markov Property (Memoryless): This property emphasizes that the future state of the system depends solely on its current situation, completely disregarding the past. In the context of our emotional state example, it means that tomorrow's emotion is influenced solely by today's emotion, without any regard for the emotional states of prior days.

Stationary Distribution: This principle suggests that over time, a Markov chain will eventually settle into a steady-state or equilibrium distribution. In this equilibrium, the probabilities of being in each state remain constant over time. In our emotional state example, this would translate to a person experiencing each of the four emotions in a certain proportion over an extended period. This is essentially their personal emotional equilibrium.

Irreducibility: Irreducibility states that it's possible to transition from any state to any other state within the Markov chain in a finite number of steps. This property ensures that the Markov chain is well-connected and allows for exploring various paths within the system. In terms of our emotional state example, it means that, regardless of your current emotional state, there's always a possibility, over time, to journey from one emotion to another. So, even after a series of sad days, there's still hope for joy.

Understanding these principles is crucial for effectively analyzing and harnessing the power of Markov Chains in practical applications. These very principles enable us to make predictions, model behaviours, and gain insights into complex systems, whether they involve emotions, finance, or other dynamic processes.

Applications of Markov Chain

Markov chains have various applications across disciplines, including statistics, computer science, finance, genetics, physics, economics and social sciences. Let's have a look at a few notable examples:

Google Search

One ubiquitous application that we all encounter regularly, yet often take for granted, is Google Search. Google's search engine utilizes the PageRank algorithm, a brainchild of its founders, Larry Page and Sergey Brin. This algorithm ranks web pages based on their significance, a metric determined by both the quantity and quality of links pointing to them. The web is modelled as a giant graph, where web pages represent states, and hyperlinks serve as transitions between these states. The probability of navigating from one page to another is precisely defined as a transition probability. Over time, this Markov process elegantly converges to a stationary distribution, yielding the coveted PageRank score for each page. The higher the score, the more "important" the page is considered to be in the vast web ecosystem.

Social Network Analysis

Social networks, whether online platforms like Facebook and Twitter or offline social structures, can be studied using Markov processes to understand and predict individual behaviours within the network.
In these networks, individuals or groups are treated as states. The probability of one individual interacting with another (e.g., forming a friendship or sharing a piece of information) is modelled as a transition probability. Over time, these probabilities can be used to predict the flow of information, the formation or dissolution of relationships, or the influence of certain individuals or groups within the network.

Text Generation

Markov chains can be used to generate text that mimics a particular style, author, or content source. This is often seen in fun applications like chatbots. By analyzing a body of text, a transition matrix is created, capturing the likelihood of one word following another. Starting with an initial word, the Markov chain can generate sequences of words that statistically resemble the source text.

And that concludes our introduction to Markov Chains. I hope you've gained a glimpse into the immense value it brings to the table.

On a personal note, I'll be taking a brief hiatus. I'm jetting off in a couple of days to recharge and explore the world, so you won't hear from me for about a month. Until then, take care and stay curious! 🤓