You know, contrary to what most people might think, math isn't really my strong suit. I've always found it kind of tough because, honestly, it can be pretty abstract and those Greek symbols just add to the confusion. Math's like a puzzle where each new piece builds on the last. I remember struggling big time with math because I didn't quite get some basic ideas. And then, of course, the class would move on to more advanced stuff, leaving me in the dust. It's like trying to build a house of cards – it will eventually collapse.

But you know what? Dealing with math struggles taught me a couple of important things. First off, practice is key to getting better. And secondly, you've got to really get what's going on under the hood. So, my approach to learning new math stuff (or anything) is to grasp the big picture and get a feel for it before diving into the nitty-gritty details, like formulas.

I used this trick to tackle Bayes' Theorem. Bayes' Theorem is a big deal in data science and AI. You've probably experienced its application. Here, let me show you.

Have you ever wondered how computers seem to know so much about us? Take this for example: if you were to search for "movie automatic shoe laces" on Google, it's likely to suggest "Back to the Future" as a result. Let me prove it to you:

But how does the search engine know this? It's not as if it has watched the movie. Instead, it understands from many similar searches that people are likely searching for. And it makes these informed guesses using something known as Bayes' Theorem.

I want to share a bit about Bayes' Theorem in this blog post. Here is what we will cover:

• What is Bayes' Theorem?
• History of Bayes' Theorem
• Breaking Down the Math
• Applications of Bayes' Theorem
• Shortcomings of Bayes' Theorem

Ready? Let's start.

What is Bayes' Theorem?

Bayes' Theorem is a statistical method for updating probabilities based on new evidence. In layman's terms, it helps us figure out the likelihood of something happening based on new information. It's like updating your belief about something when you get new evidence.

Here is an example to help cement the idea. Imagine you're trying to decide if it's going to rain tomorrow. Your friend tells you that if it's cloudy today, it's more likely to rain tomorrow. So you look outside and see that it's cloudy. Now, you're more convinced that it's going to rain tomorrow.

In this example, your initial belief is that it might rain tomorrow. The new information is that it's cloudy today. You use that new information to update your belief and conclude that it's more likely to rain tomorrow.

History of Bayes Theorem

Bayes' Theorem traces its roots back to the 18th century and is attributed to the English statistician and Presbyterian minister Thomas Bayes. He was intrigued by probability and how to make predictions with incomplete information.

Bayes developed an early version of the Theorem, but it wasn't published during his lifetime. Instead, it was introduced to the world in a paper published posthumously in 1763. Interestingly, Bayes' friend, the mathematician and preacher Richard Price, found Bayes' manuscript and recognised its significance. Price edited and presented Bayes' work to the Royal Society of London, which then published the paper, "An Essay Towards Solving a Problem in the Doctrine of Chances."

The French mathematician Pierre-Simon Laplace later refined and extended the Theorem in 1774. Laplace used the updated Theorem to tackle various scientific and mathematical challenges, notably in astronomy.

Bayes' Theorem faced criticism in its early years, mainly due to its reliance on "prior probabilities," or initial guesses about the likelihood of an event. Some viewed this requirement as subjective and unscientific. However, in the 20th century, the development of powerful computers revived interest in the Theorem, making it possible to apply it to complex, data-intensive problems.

Today, Bayes' Theorem is essential in numerous fields, including statistics, computer science, economics, and more. Its ability to update probabilities based on new evidence makes it an invaluable asset for making informed predictions and decisions in uncertain situations.

Breaking Down the Math

This is the formula:

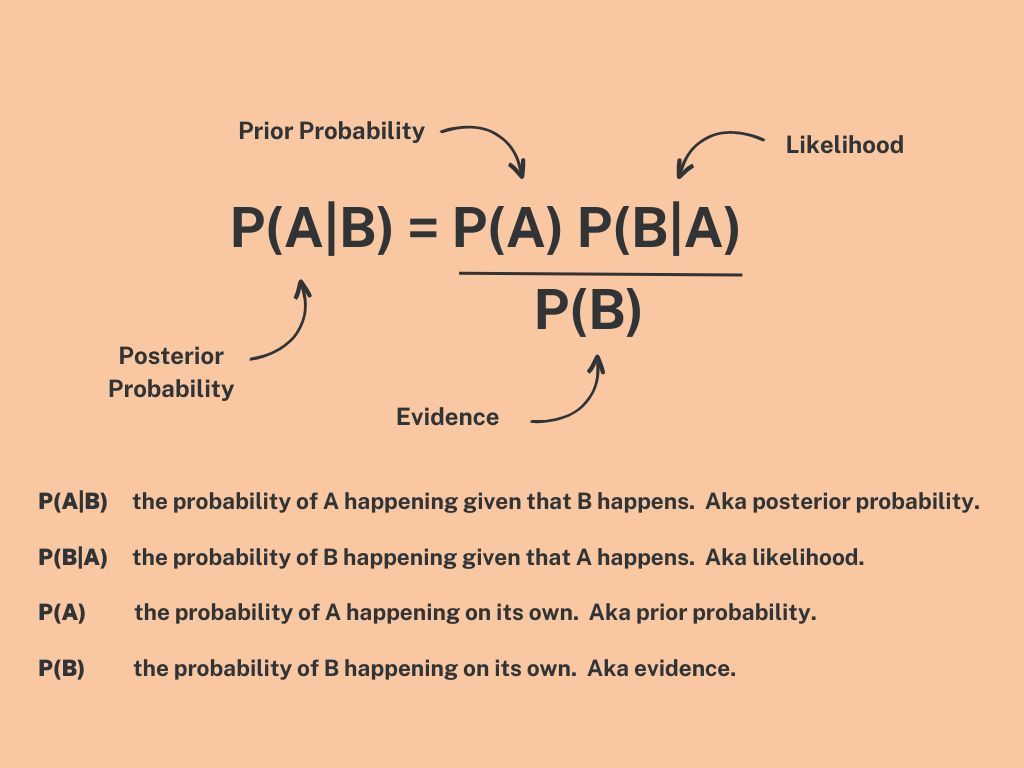
Let's look at an example. I came across this from Math is Fun. It helped me better understand the maths of Bayes' Theorem.

Imagine a party with 100 guests, and you decide to note down how many guests are wearing pink and how many are men. You come up with these numbers:

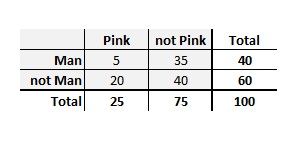
Bayes' Theorem is based on these four numbers (excluding totals).

Let's calculate some probabilities:
The probability of being a man, P(Man), is 40/100 = 0.4.
The probability of wearing pink, P(Pink), is 25/100 = 0.25.
The probability that a man wears pink, P(Pink|Man), is 5/40 = 0.125.
The probability that a person wearing pink is a man, P(Man|Pink), is...

But then, a playful puppy comes in and rips up your data! Only three values are left:
P(Man) = 0.4,
P(Pink) = 0.25, and
P(Pink|Man) = 0.125.

Can you still figure out P(Man|Pink)?

Let's say a guest wearing pink left some money behind. Was it a man? Bayes' Theorem can help answer this:

P(Man|Pink) = [P(Man) x P(Pink|Man)] / P(Pink) 
P(Man|Pink) = [(0.4 * 0.125)] / 0.25 = 0.2

We can infer that there is a 20% probability that the pink-wearing guest who left the money behind was a man.

Applications of Bayes' Theorem

Bayes' Theorem finds applications across various fields. Here are some examples:

Spam Filtering
One of the most popular methods for spam detection is the Bayesian spam filter. It uses Bayes' Theorem to calculate the probability that an email is spam based on the presence of certain words. It analyses the frequencies of words in known spam and legitimate emails.

For example, if the word "lottery" appears frequently in spam emails but rarely in legitimate emails, then a new email with the word "lottery" will have a higher probability of being classified as spam.

The Bayesian filter updates its knowledge over time as it processes more emails. If a user marks an email as spam, the filter updates its probabilities for the words in that email, making it more accurate in the future.

Risk Assessment in Lending
Banks and other financial institutions use Bayesian methods to evaluate the risk of lending money to potential borrowers. By applying Bayes' Theorem, lenders can update the probability of a borrower defaulting on a loan based on various factors, such as their credit score, income level, and employment history.

For example, consider a borrower with a low credit score. Based on prior data, the lender might initially believe there's a high probability of default. However, the borrower has a stable job with a high income. Using Bayes' Theorem, the lender can update the probability of default based on this new information, potentially making the borrower a more attractive candidate for a loan.

Bayesian methods allow lenders to continuously update their risk assessments as they receive new information about borrowers, such as their payment history or changes in employment status.

Drug Development and Clinical Trials
Researchers use Bayesian statistics to design and analyse clinical trials. Bayesian methods allow researchers to combine prior knowledge (e.g., results from earlier studies) with data from the current trial to update the probability of a drug's effectiveness.

Shortcomings of Bayes' Theorem

Bayes' Theorem is not without its flaws. Here are some of its limitations.

Reliance on Prior Probabilities
The need for a prior probability is a key feature of Bayesian statistics, but it can also be a drawback. Before considering any new evidence, the prior represents our initial beliefs about an event. But selecting an appropriate prior can be challenging. If the prior is not representative of the true state of the world, it can heavily influence the outcome and lead to inaccurate conclusions.
For example, if a medical test is being used in a population where a disease is extremely rare, the prior probability of the disease will be low, which can impact the test results' accuracy.

Computational Complexity
Bayesian methods can be computationally demanding, especially when dealing with large datasets or complex models. This can make it challenging to implement Bayesian techniques in real-time applications or situations where computational resources are limited. As datasets become larger, the calculations required for Bayesian methods can become increasingly time-consuming and resource-intensive.

Assumption of Independence
Bayes' Theorem assumes that the evidence is independent of the event, given the conditions. This assumption is often called the "independence assumption." However, in real-world scenarios, this assumption may not always hold. For example, in medical diagnosis, symptoms are often correlated with each other. In such cases, the independence assumption can lead to calculation inaccuracies.

Subjectivity
Bayesian statistics incorporates subjective beliefs into the analysis. While this allows for the inclusion of expert knowledge, it also introduces a degree of subjectivity into the results. Different analysts with different prior beliefs may arrive at different conclusions based on the same evidence. This subjectivity can make it challenging to achieve a consensus among experts and impact the results' generalizability.

Overconfidence
In some cases, using Bayesian methods can lead to overconfidence in the results. Because Bayesian statistics allows for the incorporation of prior beliefs, there is a risk of over-relying on prior knowledge and ignoring new evidence. This can result in overconfidence in the conclusions and a reluctance to update beliefs in the face of new evidence.

Despite these shortcomings, Bayes' Theorem remains a powerful tool for updating probabilities based on new evidence. It is widely used in various fields, from medicine to finance to artificial intelligence. However, it is essential to be aware of the limitations and assumptions of Bayesian methods and to use them appropriately and cautiously.

To sum it up, Bayes' Theorem is an impressive tool for fine-tuning probabilities using new information, and it's a big deal in data science. Even though it has some limitations, it's super handy for figuring things out in a world full of unknowns. It's like a secret weapon for making smarter choices using new facts.